contoh soal vektor
Soal 1
Diketahui dua buah vektor masing-masing |ā| = 2 dan |b̄| = 1. Jika sudut antara kedua vektor adalah 60° maka |ā + b̄| sama dengan….
A. √3
B. √5
C. √6
D. √7
E. √11
Pembahasan
Penjumlahan dua buah vektor, cos 60° = 1/2. Misal hasilnya adalah c̄:
|c̄|2 = |ā|2 + |b̄|2 + 2|ā||b̄| cos θ
|c̄|2 = (2)2 + (1)2 + 2(2)(1)(1/2);
|c̄|2 = 4 + 1 + 2
|c̄|2 = 7
|c̄| = √7
Soal 2
Diketahui dua buah vektor masing-masing |p̄| = 2 dan |q̄| = 1. Jika sudut antara kedua vektor adalah 120° maka |p̄ − q̄|2 sama dengan….
A. 5
B. 6
C. 7
D. 8
E. 9
Pembahasan
Pengurangan dua buah vektor:
|p̄ − q̄|2 = |p̄|2 + |q̄|2 − 2|p̄||q̄| cos θ
Dengan
cos 120° = −1/2
|p̄ − q̄|2 = (2)2 + (1)2 − 2(2)(1)(−1/2)
|p̄ − q̄|2 = 4 + 1 + 2
|p̄ − q̄|2 = 7
Jawaban: C. 7
Soal 3
Tiga buah titik P, Q, dan R terletak pada satu garis. Jika P (1, 2, −1), Q (3, 0, 2) dan R (7, −4, 2b + 1), maka nilai b sama dengan….
A. 3/2
B. 5/2
C. 7/2
D. 9/2
E. 11/2
Pembahasan
P, Q, dan R dalam satu garis maka berlaku:
PQ = k ⋅ QR
Dimana PQ = Q − P dan QR = R − Q
P (1, 2, −1), Q (3, 0, 2) dan R (7, −4, 2b + 1)
2 = k(4)
Terlihat bahwa k = 2/4 = 1/2 sehingga
3 = k(2b – 1 )
3 = 1/2(2b – 1)
6 = 2b – 1
2b = 7
b = 7/2
Jawab: B. 7/2
Soal 4
Jika vektor-vektor p̄ = (x + 1) i -5j + k dan q̄ = -7i – 2j + (y + 2)k saling tegak lurus, maka berlaku….. (matematika123.com_2020)
A. y = 3x – 5
B. y = 4x – 5
C. y = 5x – 5
D. y = 6x – 5
E. y = 7x – 5
Pembahasan
Dua buah vektor saling tegak lurus maka berlaku p̄ ⋅ q̄ = 0
(x + 1)(-7) -5(-2) + 1(y + 2) = 0
-7x – 7 + 10 + y + 2 = 0
-7x + y + 5 = 0
y = 7x – 5
Jawaban: E. y = 7x – 5
Soal 5
Diberikan tiga buah vektor masing-masing sebagai berikut:
p = i + j + k
q = 2i – 3j +k
r = – 2j – 3k
Jika s = 2p – q + 3r, maka s =….
A. i + 2j -7k
B. – i + 6k
C. 6i + 7k
D. – j – 8k
E. j + 4k
Pembahasan
p = i + j + k
q = 2i – 3j +k
r = – 2j – 3k
Menentukan vektor s, harus teliti dengan tanda positif dan negatif dalam soal.
s = 2p – q + 3r
= 2(i + j + k) – (2i – 3j +k) + 3(– 2j – 3k)
= 2i + 2j + 2k – 2i + 3j – k – 6j – 9k
= 2i – 2i + 2j + 3j – 6j + 2k – k – 9k
s = – j – 8k
Soal 6
C adalah proyeksi vektor ā pada b̄. Jika ā = 2i + j dan b̄ = 3i + 4j, maka c̄=….
A. 1/5 (3i + 4j)
B. 2/5 (3i + 4j)
C. 4/25 (3i + 4j)
D. 2/25 (3i + 4j)
E. 1/25 (3i + 4j)
Pembahasan
Rumus proyeksi vektor ortogonal:
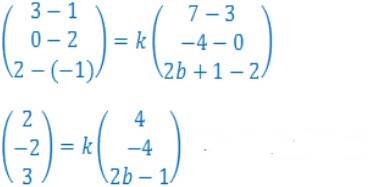
Soal 7
Diketahui segitiga PQR dengan P(1, 4, 6), Q(1, 0, 2) dan R(2, –1, 5). Titik A terletak pada perpanjangan PQ sehingga PA : QA = 3 : 1. Panjang vektor yang diwakilkan oleh AR adalah…
A. 3
B. √13
C. 3√3
D. √35
E. √43
Pembahasan
Perhatikan gambar!
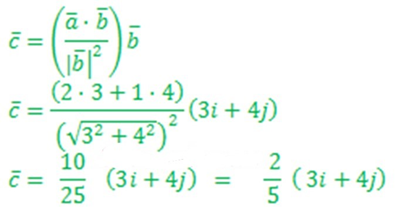
Titik P, titik Q dan titik A segaris (kolinier) dengan perbandingan PQ : PA = 2 : 3.
Sehingga berlaku:
PQ = 2/3 PA
Misalkan A (a, b, c )

Diperoleh tiga persamaan masing-masing:
0 = 2/3 (a – 1)
-4 = 2/3 (b – 4)
-4 = 2/3 (c – 6)
Diperoleh nilai a, b dan c berturut-turut adalah:
a = 1, b = -2 dan c = 0
Sehingga titik A = (1, -2, 0)
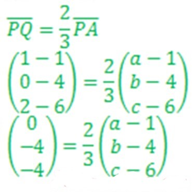
Panjang AR dengan demikian adalah:
A = (1, -2, 0)
R = (2, –1, 5)
|AR| = √([2 – 1]2 + [ – 1 – ( -2)]2 + [5 – 0]2)
= √(1 + 1 + 25)
= √(27) = 3√3
